磁歪材料による環境振動発電

Daniele Davino

Department of Engineering University of Sannio, 82100 Benevento, Italy

はじめに

ウェアラブル電子機器やワイヤレスセンサの利用が制限されている大きな要因は、内蔵電池に蓄積できるエネルギー量に限りがある点にあります。現時点での最も一般的な対策としては、必要な時に充電／再充電する方法ですが、実用的にも経済的にも最適とはいえません。例えば、遠隔地やアクセスしにくい場所にあるリモートワイヤレスセンサの電池交換や再充電には、資格を有する技術者がセンサのある場所に行く必要があり、維持コストが著しく高くなってしまいます。

環境発電（energy harvesting）は、現代のワイヤレス電子機器のコンセプトを実現するための重要な手法になる可能性を秘めています¹。適切な多機能材料の特性を利用することで、環境からエネルギーを「収穫、ハーベスト」することが可能です。例えば、磁歪（じわい）材料や圧電材料は、機械的もしくは熱的エネルギーを電気的・磁気的エネルギーに直接変換することができます。

本論文では、磁歪材料を用いた環境発電の物理、工学、および応用について解説します。これらのデバイスは、その性質が材料特性に強く依存しているため、概念的にはシンプルです。そのため、材料特性を最適化することによってデバイス性能を改善できます。

磁歪材料（もしくは、一般的には磁気弾性材料）は、巨視的な機械的変数（応力σ と歪ε ）、磁場Hおよび磁束密度Bの間に無視できない関係を示すという特異な特性を持っています^2,3。この特性はアクチュエーションを得るために利用され、「磁歪」と呼ばれる、適切な磁場の印加による巨視的な伸縮が得られます。磁歪効果は、鉄やニッケルなどの一般的な材料にも見られますが、それらの巨視的な効果（寸法変化）はそれぞれ約12 ppmと-50 ppmと限られたものです。正の磁歪は伸び、負の磁歪は収縮を示します。Terfenol（テルビウム-ジスプロシウム-鉄合金）^5,6、Galfenol（ガリウム-鉄合金）⁷、Alfenol（アルミニウム-鉄合金）⁸のような合金は、変化量が最大2,000 ppmもの超磁歪現象（giant magnetostriction）を示します。なお、磁歪材料の詳細については参考文献2をご覧ください。この磁気的効果は逆方向にも利用され、「ビラリ効果（Villari effect）」⁴（もしくは逆磁気弾性効果）と呼ばれます。

この場合、周期的な機械的応力を磁歪材料に加えることによって周期的な磁化が発生します。この効果は、ファラデー－ノイマン誘導法則のために時間をかけて得られるため、材料の周りに巻いたピックアップコイルに誘導電圧が生じ、周期を速めると電圧が上昇します。この現象が、磁歪材料による環境振動発電（KEH：kinetic energy harvesting）の原理になります。周囲環境の振動を応力の変化にうまく変換することができた場合、この技術によって振動エネルギーを電気エネルギーに変換することができます。

本論文では、まず、磁歪材料の主だった巨視的特性について解説します。次に、磁歪材料を用いたKEHの原理、および関連する材料特性を紹介します。

磁歪材料の挙動

磁歪材料には、共通する巨視的特性がいくつかあります。図1に、Terfenol-d ロッドの単軸性磁歪挙動を示します。ここではロッドの軸方向に印加した磁場に沿った磁歪効果を測定しています。図1Aに磁歪曲線（ε 対 H）を示します。ここでは、1）ヒステリシス、2）Hに対して対称な挙動（butterfly wings、2枚の蝶の羽根のような形）、3）印加した圧縮応力に応じて曲線の形状が依存するという3つの特徴が見られています。特に、印加した圧縮応力と曲線の関係がやや複雑な点に注意する必要があります。図1Bに、ビラリ効果のもたらす、さまざまな磁場を印加したときのB 対 σ のプロットを示します。ここでも、ヒステリシス（磁気誘導が極めて小さなH = 0 kA/mの場合を除く）と印加した応力および磁場に関する複雑な挙動に注意する必要があります。後者の特性は、材料のエネルギー回収の可能性を推測する上で重要です。実際、ある応力変動Δσでの磁気誘導変動ΔBが大きいほど、エネルギー変換が高くなります。条件が同じであれば、Galfenolのような異なる磁歪材料も同様の挙動を示します。

図1A）さまざまな圧縮応力でのTerfenol-d ロッドの磁歪特性。B）異なる磁場における、周期的な圧縮応力による周期的磁気誘導（ビラリ効果）

デバイスの機械的インピーダンス整合もKEH用磁歪材料の重要な特性です。TerfenolやGalfenolなどの材料は非常に高い剛性を示し、バルク鉄に近い機械挙動を示します（図2）。その理想的な振動は、高い応力と低い歪（0～1,000ppmの範囲）で得られます。より柔らかい磁気弾性材料であれば、ゴムのような挙動により、より低い応力と高い歪（0.1～1%の範囲）の振動エネルギーを回収できるはずです。

Metglassと呼ばれる磁気弾性材料も、環境発電用材料として検討されています^9,10。その主な利点は、積層することによってエネルギー密度が向上する点にあります。Metglassは、優れた軟磁気特性と弾性応答を示すFe系アモルファスリボンで、原理的にはFe-Ga合金やFe-Tb-Dy合金より低コストで製造できます。

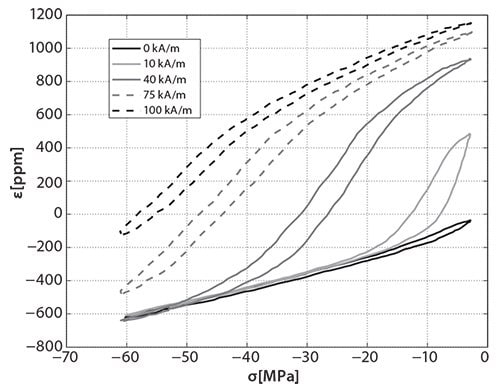
図2様々な一定磁場におけるTerfenol-d ロッドの機械特性

環境振動発電デバイス

磁歪材料を基盤とした環境振動発電デバイスの動作原理はビラリ効果に由来しており、十分な効果を得るには、周囲環境からエンドユーザーまでの間にいくつかの機能性コンポーネントが必要になります（図3）。環境振動を磁歪材料に伝えるには適切な機械的構造が必要であり、力学的エネルギーの伝達を最大化するためにはその設計が極めて重要になります。

図4に、機械的パーツの実装についての2つのコンセプトを表した概念図を示します。図4Aは、振動源と固定部の間に活性材料を使用した方法です¹¹。磁歪材料ロッド（灰色）は固定部と接合され、時間変動する均一な力が軸方向に加わります。そのため、z軸方向に圧縮応力が発生し、時間によって磁化量が変動します。図4Bは、振動する部品を用いる場合に適しています¹²。この場合、磁歪カンチレバー（梁）の一端は振動部と強固に結合され、一方の端はそれより重い物質と接合しています。この錘に振動が誘導されるため、梁に対して垂直方向の応力が働き、磁化量が時間によって変動します。なお、磁歪材料の周囲に巻かれたコイルと、磁束線の（閉じた）通路となる磁気回路（図4では省略）が、いずれの方法でも共通して必要となります。

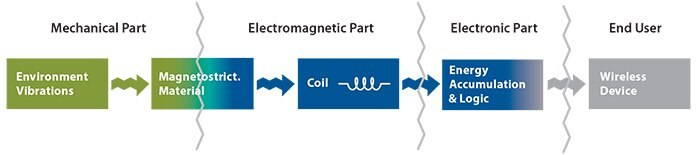
図3磁歪材料による環境振動発電に関する各プロセスの概念図

図4磁歪材料による環境振動発電の2つの概念図：A）force-driven、B）velocity-driven

いずれの方法にも利点があります。図4A方式の場合、周波数に下限はないもの、一般的には図4B方式より大型のシステムになります。図4B方式の場合、梁と錘を用いたシステムに固有の共振挙動のためにパスバンド周波数を持ち、系の共振周波数周辺の振動において最も有効に作動します。もちろん、動作周波数帯の拡大によってこの問題を回避する試みがすでに行われています¹³。

図3は、電気エネルギーの最適化（安定化）と蓄積を目的とした電子回路部分（Electronic part）が、発電デバイスの「電気的負荷（electric load）」にあたることを示しています。磁歪材料を用いたKEHデバイスの開発はまだ初期段階にありますが、圧電物質ベースのKEHデバイスに関しては、すでに多くの研究と応用開発が行われています¹⁴。一般に、運動エネルギーを利用した環境発電デバイスは、電気エネルギー蓄積のために適切な回路技術と組み合わせる必要のある、不安定なAC電源です。さらに、磁歪材料に特有の性質があるものの、原理的には、すでに圧電物質ベースのデバイスに対する開発に、必要な変更を加えることで開発が可能であると考えられます。

この系はまた、バネ‐質量‐減衰系として考えることによって、電気的‐機械的観点から理解することもできます。ビラリ効果によっても機械的エネルギーの一部が消費されるため、減衰は機械的摩擦とエネルギー回収の両方において起こります¹⁵。磁歪材料は、一種の電気‐機械エネルギーの変換器（一次側：相補的な力学量（力と速度）、二次側：コイル端子における相補的な量（電圧と電流））として動作します¹⁶。電圧v(t)は、磁気誘導の変化率∂B/∂tと一般的な幾何的および磁気的パラメーター（コイルの巻き数、コイルの面積、磁気回路特性など）に比例します。この特性を利用して次の関係が導かれます（式1）。

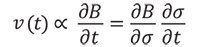
∂σ/∂tの項は振動の周波数と関係し、振動源によって制御されます。初めの項は、「圧磁係数（piezo-magnetic coefficient）」と呼ばれる材料固有の特性であり、次のセクションで解説します。

圧磁係数

圧磁係数は次の式で定義されます（式2）^17,18。

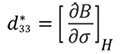
つまり、この値は定数Hにおけるσに関するBの変化率です。このパラメータは通常、材料のデータシートや線形モデルでは一定とみなします¹⁸。このような近似が許容されるケースはいくつかあります。たとえば、最大許容外部応力より大きな機械的予応力（prestress：機械的な圧縮応力をあらかじめ与えておくこと）がデバイスに印加されているようなアクチュエータに磁歪材料が使われている場合です¹⁹。一方、環境発電用途のケースのように未知の動的条件を考慮する場合は一般的な定義を利用しなければなりません。圧磁パラメータは材料特性に固有の導関数であり、(H, σ)対に関して非線形である上、ヒステリシスを示します。それにもかかわらず、この値は実験で得られたヒステリシス・ループの数値微分から得ることができます¹⁷。この演算をTerfenol-dロッドで行った結果を図5に示します。この値は、文献20で報告されているように10^-8 m/Aの領域にありますが、一定ではなく、(H, σ)対に強く依存しています。最大ピークは、高いσほど高い磁場（H）に移動していますが、これは非線形モデルの結果を裏付けるものです¹¹。σ∈(-10,0) MPaとH∈(10,20) kA/mの範囲では、相対的に低いσとHで最大値に達しています。これら値はデバイスの最適化に有用であり、最適な磁気バイアスおよび機械的予応力の選択に用いられます。このように、磁歪材料をベースとするKEHデバイスには、圧磁パラメータに関して最適な条件を得るために、磁気バイアス（たとえば磁気回路中の永久磁石）や、静的予応力を印加する装置²¹が必要であることを示しています。

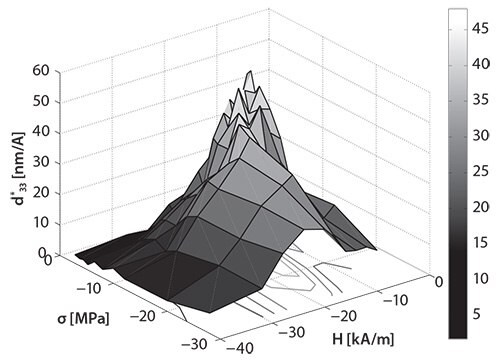
図5Terfenol-d ロッドの圧磁係数。参考文献17より転載

エネルギー回収サイクルの最適化

KEHデバイスのエネルギー密度は、B-H 平面内のB-H サイクルで囲まれた領域に基づいて計算することができます（図6）。この面積は、時計回りのサイクルではエネルギー利得を、反時計回りのサイクルではエネルギー損失を表します。磁気バイアスや予応力などのパラメータを適切に選択し、B-H サイクルで囲まれた面積を最大化することによって、KEHデバイスを効果的に最適化できます。

一定応力下で得られた材料の磁気サイクルに関して、B-H 平面での時計回りのサイクル挙動を調べると興味深いことが分かります。図6Aのプロットは、1.58 MPaと48.2 MPaの一定応力でのGalfenolロッドの反時計回りの磁気特性を示しています。また、サイクル内の線は、1 MΩの単純な抵抗を電気負荷として用いた場合の発電テストで得られた、時計回りのループを表しており、周期的な応力変動はσ = 1.58 MPa～48.2 MPa（周期は1.25s）、3通りの磁場バイアス（8.7 kA/m：オレンジ、14.8 kA/m：茶色、および23 kA/m：赤）の場合を示しています。さまざまなバイアス場で得られたB-H ループが、理論的に予測された磁気特性の範囲内にあることが分かります²²。さらにこれは、H = 14.8 kA/mで異なる値の抵抗を用いた図6Bでも成り立ちます。抵抗が小さいほど、ピックアップコイルを循環する電流が増えて磁場変動も大きくなるため、B-H ループが広くなります。この結果は、材料のエネルギー回収特性を改善するにあたって、限定されたサイクル内で利用可能な面積を大きくするために、さまざまな応力下での静的磁気特性にできるだけ集中すべきことを示しています。

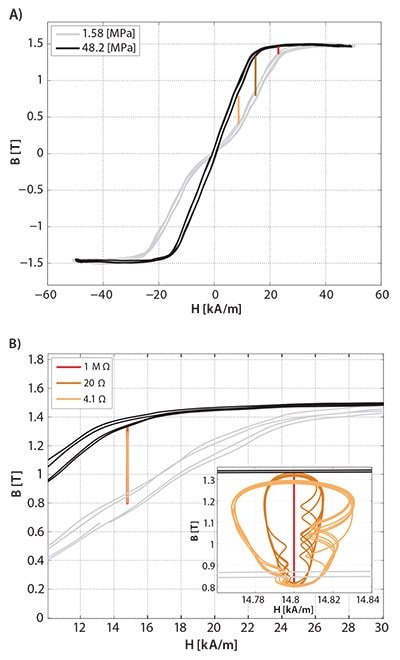
図61.58 MPa（黒）と48.2 MPa（グレー）の一定応力でのGalfenolロッドの磁気特性。A）エネルギー回収サイクルT = 1.25s、H = 8.7 kA/m：オレンジ、H = 14.8 kA/m：茶色、およびH = 23 kA/m：赤、R = 1 MΩ　B）エネルギー回収サイクル：T = 1.25s、R = 4.1Ω：オレンジ、R = 20Ω：茶色、およびR = 1 MΩ：赤

結論

磁歪材料を用いた環境振動発電デバイスは、一定応力の印加のもと、その性能は、圧磁係数やB-H 磁気サイクル挙動といった特性から主に影響を受けるシンプルなデバイスです。改善された新規材料によって、環境発電性能を向上できる可能性があります。デバイスの巨視的分析から、研究の重点を圧磁係数の最大化に置き、B-H 平面内の静的サイクルにおけるエネルギー回収サイクルの最適化が必要があることが示唆されます。

謝辞

本研究は、イタリア研究プロジェクトPON “Low Noise” grant（PON01-1878）の支援を受けました。

References

Eds KB. 2011. Energy Harvesting Systems. New York: Springer.

Engdahl G. 2000. Modeling of Giant Magnetostrictive Materials.127-205. https://doi.org/10.1016/b978-012238640-4/50018-8

Ed dTdL. 2005. Magnetism – Materials and Applications, Vol. II,. New York: Springer.

Lee EW. 1955. Magnetostriction and Magnetomechanical Effects. Rep.Prog.Phys.. 18(1):184-229. https://doi.org/10.1088/0034-4885/18/1/305

Clark AE, Teter JP, McMasters OD. 1988. Magnetostriction "jumps" in twinned Tb0.3Dy0.7Fe1.9. Journal of Applied Physics. 63(8):3910-3912. https://doi.org/10.1063/1.340602

Clark A, Wun-Fogle M, Restorff J, Lindberg J. 1992. Magnetomechanical properties of single crystal TbxDy1-x under compressive stress. IEEE Trans.Magn.. 28(5):3156-3158. https://doi.org/10.1109/20.179743

Clark AE, Hathaway KB, Wun-Fogle M, Restorff JB, Lograsso TA, Keppens VM, Petculescu G, Taylor RA. 2003. Extraordinary magnetoelasticity and lattice softening in bcc Fe-Ga alloys. Journal of Applied Physics. 93(10):8621-8623. https://doi.org/10.1063/1.1540130

Davis CM, Ferebee SF. 1956. Dynamic Magnetostrictive Properties of Alfenol. The Journal of the Acoustical Society of America. 28(2):286-290. https://doi.org/10.1121/1.1908263

Wang L, Yuan FG. 2008. Vibration energy harvesting by magnetostrictive material. Smart Mater.Struct.. 17(4):045009. https://doi.org/10.1088/0964-1726/17/4/045009

10.

Zucca M, Bottauscio O, Beatrice C, Fiorillo F. 2011. Modeling Amorphous Ribbons in Energy Harvesting Applications. IEEE Trans.Magn.. 47(10):4421-4424. https://doi.org/10.1109/tmag.2011.2158301

11.

Davino D, Giustiniani A, Visone C. 2009. Capacitive Load Effects on a Magnetostrictive Fully Coupled Energy Harvesting Device. IEEE Trans.Magn.. 45(10):4108-4111. https://doi.org/10.1109/tmag.2009.2021671

12.

Davino D, Giustiniani A, Visone C. 2011. A Two-Port Nonlinear Model for Magnetoelastic Energy-Harvesting Devices. IEEE Trans.Ind. Electron.. 58(6):2556-2564. https://doi.org/10.1109/tie.2010.2062477

13.

Ueno T, Yamada S. 2011. Performance of Energy Harvester Using Iron-Gallium Alloy in Free Vibration. IEEE Trans.Magn.. 47(10):2407-2409. https://doi.org/10.1109/tmag.2011.2158303

14.

Cottone F, Vocca H, Gammaitoni L. Nonlinear Energy Harvesting. Phys.Rev. Lett.. 102(8): https://doi.org/10.1103/physrevlett.102.080601

15.

Guyomar D, Lallart M. Recent Progress in Piezoelectric Conversion and Energy Harvesting Using Nonlinear Electronic Interfaces and Issues in Small Scale Implementation. Micromachines. 2(2):274-294. https://doi.org/10.3390/mi2020274

16.

Davino D, Giustiniani A, Visone C, Adly A. 2011. Experimental analysis of vibrations damping due to magnetostrictive based energy harvesting. Journal of Applied Physics. 109(7):07E509. https://doi.org/10.1063/1.3545798

17.

Davino D, Giustiniani A, Visone C. 2011. A Two-Port Nonlinear Model for Magnetoelastic Energy-Harvesting Devices. IEEE Trans.Ind. Electron.. 58(6):2556-2564. https://doi.org/10.1109/tie.2010.2062477

18.

Davino D, Giustiniani A, Visone C. 2012. The piezo-magnetic parameters of Terfenol-D: An experimental viewpoint. Physica B: Condensed Matter. 407(9):1427-1432. https://doi.org/10.1016/j.physb.2011.05.059

19.

Moffett MB, Clark AE, Wun-Fogle M, Linberg J, Teter JP, McLaughlin EA. 1991. Characterization of Terfenol-D for magnetostrictive transducers. The Journal of the Acoustical Society of America. 89(3):1448-1455. https://doi.org/10.1121/1.400678

20.

Kellogg R, Flatau A. 2004. Wide Band Tunable Mechanical Resonator Employing the ΔE Effect of Terfenol-D. Journal of Intelligent Material Systems and Structures. 15(5):355-368. https://doi.org/10.1177/1045389x04040649

21.

Zhao X, Lord DG. 2006. Application of the Villari effect to electric power harvesting. Journal of Applied Physics. 99(8):08M703. https://doi.org/10.1063/1.2165133

22.

Davino D, Giustiniani A, Visone C. Magnetoelastic Energy Harvesting: Modeling and Experiments. https://doi.org/10.5772/50892

23.

Davino D, Giustiniani A, Visone C. 2009. Analysis of a magnetostrictive power harvesting device with hysteretic characteristics. Journal of Applied Physics. 105(7):07A939. https://doi.org/10.1063/1.3077208

ログインして続行

続きを確認するには、ログインするか、新規登録が必要です。

アカウントをお持ちではありませんか？