Oligonucleotide Melting Temperature
How do you calculate the Tm of DNA?
The melting temperature (Tm) of an oligonucleotide is the temperature at which 50% of the oligonucleotide is duplexed with its perfect complement and 50% is free in solution. Awareness of the Tm is critically important for numerous techniques in molecular biology (e.g., PCR, Southern blotting, in situ hybridization). Some of these classic techniques are still widely used in conjunction with newer techniques, such as PCR-based library preparation of samples to be used in next-generation sequencing.
The most common experimental method for determining Tm is to measure the absorbance change of the oligonucleotide with its complement as a function of temperature (Figure 1). While experimentally-determined Tm values are the most accurate, they are not necessary when using classic molecular techniques for routine applications.

Figure 1. Example of experimental determination of oligonucleotide Tm. Measurements are made in a thermostatted cell in a UV-Vis spectrophotometer. The Tm is the reading halfway between the double-stranded DNA (dsDNA) and single-stranded DNA (ssDNA) plateaus.
Theoretical methods that take into account the likely intended technique as well as factors affecting melting (sequence concentration, sequence length, base composition, ionic strength, etc.) can be used to calculate the expected Tm.
Theoretical DNA Tm Calculation Methods
Depending on the nature of the sequence, we use one of two methods to calculate Tm:
- Nearest Neighbors
- Basic
Nearest Neighbors
The primary method we use to calculate Tm is the nearest neighbors method1,2, and we use it for oligonucleotides with sequence lengths from 15 to 120 bases (upper length limit of our standard DNA oligos offering). This method is considered to be the most accurate as it takes into account the sequence of the oligonucleotide rather than just the base composition as the other method does. The nearest neighbors method accounts for thermodynamic as well as other factors that affect Tm, including oligonucleotide and monovalent cation concentrations.
We use the following modified nearest neighbors formula:

Where:
Tm = melting temperature in °C
ΔH = enthalpy change in kcal mol-1 (accounts for the energy change during annealing / melting)
A = constant of -0.0108 kcal K-1 ᐧ mol-1 (accounts for helix initiation during annealing / melting)
ΔS = entropy change in kcal K-1 ᐧ mol-1 (accounts for energy unable to do work, i.e. disorder)
R = gas constant of 0.00199 kcal K-1 ᐧ mol-1 (constant that scales energy to temperature)
C = oligonucleotide concentration in M or mol L-1 (we use 0.0000005, i.e. 0.5 µM)
-273.15 = conversion factor to change the expected temperature in Kelvins to °C
[Na+] = sodium ion concentration in M or mol L-1 (we use 0.05, i.e. 50 mM)
There are a finite number of nearest-neighbor values for ΔH, ΔS, and A, which can be plugged directly into the above formula (Table 1).
Table 1. Nearest-neighbor values for ΔH and ΔS. In the paper that serves as the source for the base nearest neighbors formula (Reference 1), ΔS, A, and R are reported in units of cal K-1 ᐧ mol-1, so a factor of 1,000 is multiplied by ΔH (reported in kcal mol-1) in the formula to balance the units. Here we report ΔS, A, and R in units of kcal K-1 ᐧ mol-1 so that the units for each parameter match, and therefore, make the example calculation below more intuitive to follow during dimensional analysis. Regardless of approach, the calculated Tm is identical. For a complete list of ΔH and ΔS values, including for wobble sequences, please contact our technical services group at oligotechserv@sial.com.
*The left sequence is 5' to 3', while the right sequence is 3' to 5', e.g. for AA/TT, AA is 5' to 3' and TT is 3' to 5'. When selecting values, always choose in the 5' to 3' direction, regardless of whether it is the left or right sequence in the correct orientation.
**Negative values reflect that annealing is enthalpically and entropically favorable. Positive values would reflect the reverse reaction, melting, and would lead to an identical Tm calculation.
Nearest Neighbors Example Calculation. This example will demonstrate the manual calculation of the Tm for the following sequence:
5'-AAAAACCCCCGGGGGTTTTT-3'
This is the above sequence paired with its reverse complement:
5'-AAAAACCCCCGGGGGTTTTT-3'
3'-TTTTTGGGGGCCCCCAAAAA-5'
Step one: identify nearest neighbor values for ΔH and ΔS and sum each parameter
Reading the target sequence 5' to 3', ΔH and ΔS values for all nearest neighbors can be found in Table 1. The identified nearest neighbor pairs along with their ΔH and ΔS values (and sums) are as follows:
Step two: plug values into nearest neighbors formula to calculate melting temperature

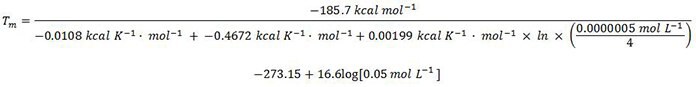
Tm = 69.6 °C
As a comparison, here is the value as determined by an online oligonucleotide sequence calculator:

The manually calculated value of 69.6 and the online calculator calculated value of 69.7 (the discrepancy is because the original literature value for the gas constant of 1.987 was rounded to 1.99 for this example calculation).
The value of 69.7 would be displayed on the technical datasheet provided with this oligonucleotide.
Basic
A secondary method we use to calculate Tm is the basic method (a modified Marmur Doty formula3), which we use for oligonucleotides with short sequences lengths, i.e. those that are 14 bases or less. Partly derived from membrane hybridization experiments, this method assumes a primer concentration of 50 nM, a monovalent (Na+) ion concentration of 50 mM, and pH 7.0. Given that membrane hybridization experiments are not as commonly conducted these days as was the case decades ago when this research was originally conducted, a correction factor accounts for the oligonucleotide likely being free in solution, e.g. used in a more contemporary technique, such as PCR.
We use the following modified Marmur Doty formula:
Tm = 2(A + T) + 4(C + G) - 7
Where:
Tm = melting temperature in °C
A = number of adenosine nucleotides in the sequence
T = number of thymidine nucleotides in the sequence
C = number of cytidine nucleotides in the sequence
G = number of guanosine nucleotides in the sequence
-7 = correction factor accounting for in solution
Marmur Doty Example Calculation. This example will demonstrate the manual calculation of the Tm for the following sequence:
5'-ACGTCCGGACTT-3'
Step one: plug values into Marmur Doty formula to calculate melting temperature
Tm = 2(A + T) + 4(C + G) - 7
Tm = 2(2 + 3) + 4(4 + 3) - 7
Tm = 31.0 °C
As a comparison, here is the value as determined by an online oligonucleotide sequence calculator:

The value of 31.0 would be displayed on the technical datasheet provided with this oligonucleotide.
If you intend to use such short oligonucleotides for membrane hybridization experiments, we encourage addding +7 manually to the displayed Tm, (i.e., the above value would be 38 °C).
Conclusion
One of two methods is used to determine the Tm of an oligonucleotide, and it is optimized for classic molecular techniques. If additional help is needed, please consult our technical services group.
References
To continue reading please sign in or create an account.
Don't Have An Account?